This post we will summarize the deep deterministic policy gradient (DDPG) algorithm, to see how it works in continuous action space and how the Deep Q Learning and Deterministic Policy Gradient algorithm are combined. This post is organized as follow:
1. DDPG overview, what’s the goal of DDPG and the problem of DQN;
2. Formulation of DDPG, its derivation and solution;
3. DDPG Implementation.
1. DDPG Overview
DDPG is an actor-critic, model-free algorithm based on the deterministic policy gradient that can operate over continuous action space. DDPG combines the deterministic policy gradient (DPG) and Deep Q-learning (DQN). DDPG concurrently learns a Q-function and a policy. It uses off-policy data and the Bellman equation to learn the Q-function, and uses the Q-function to learn the policy.
Problem of DQN:
DQN solves problems with high-dimensional observation spaces and can only handle discrete and low-dimensional action spaces. In tasks like physical control tasks that have continuous (real valued) and high dimensional action spaces.
Any way to solve the ‘infinite action’ problem in DQN?
One alternative method is discretizing the action space, but this will lead to an action space with dimensionality, and is not suitable for tasks that require a finer grained discretization, leading to an explosion of the number of discrete actions (too large); meanwhile, it throws away information about the structure of the action domain (not precise), which may be essential for solving many problems.
Conclusion : DQN focuses on solving the tasks of high-dimensional observation spaces, while DDPG focuses on solving the tasks of high-dimensional action spaces.
Goal of DDPG:
DQN solves problems with high-dimensional observation spaces, it can only handle discrete and low-dimensional action spaces. DQN cannot be straightforwardly applied to continuous domains since it relies on a finding the action that maximizes the action-value function, which in the continuous valued case requires an iterative optimization process at every step. (Discretizing the action space will lead to an action space with dimensionality or lead to an explosion of the number of discrete actions, and throws away information meanwhile.
In Q-learning, if you know the optimal action-value function ![]() , then in any given state, the optimal action
, then in any given state, the optimal action ![]() can be found by solving
can be found by solving
![]()
Because the action space is continuous, the function
Idea behind: using a new neural network to approximate the max calculation.
Recap:
DQN solves the problem of learning large, no-linear function approximators, which was generally believed to be difficult and unstable by introducing two innovations:
• The network is trained off-policy with samples from a replay buffer to minimize correlations between samples;
• The network is trained with a target Q network to give consistent targets during temporal difference backups.
DDPG reuses the replay buffer and target network ideas, meanwhile, it incorporates the batch normalization trick, which does not exist in original DQN, to solve the problem of generalization for input observation scaling. According to the DDPG paper, it can learn competitive polices for all tasks researched of low-dimensional observations, and some of the high-dimensional observations like pixels, but not all (to be proved).
Key Features:
• Compared with DPG algorithm, DDPG is inspired by the success of DQN, allowing to use deep neural network function approximators to learn in large state and action spaces online.
• Introduce batch normalization to normalize each dimension of observations across the samples in a minibatch to have unit mean and variance, thus to make the network easy to learn effectively and easy to find hyper-parameters which generalize across environments with different scales of state values.
• Solving the issue of the exploration in continuous action spaces by adding noise sampled from a noise process, namely, the Ornstein-Uhlenbeck process. (The OpenAI Spinning up document mentions the random Gaussian noises works well too)
• Introducing the replay buffer as in DQN to handle the problem of training neural network using samples generated from exploring sequentially in an environment that are not independently and identically distributed.
• Introduce the target network for both the actor and the critic to improve the stability of learning. By using “soft” target updates, a copy of the actor and critic networks is created and used for calculating the target values, rather than directly copying the weights.
Quick Facts:
• DDPG is an off-policy algorithm.
• DDPG extends DPG to Deep RL.
• DDPG can only be used for environments with continuous action spaces.
• Off-policy with Actor-Critic architecture for continuous action spaces.
• DDPG can be thought of as being deep Q-learning for continuous action spaces.
• DQN focuses on solving the tasks of high-dimensional observation spaces, while DDPG focuses on solving the tasks of high-dimensional action spaces.
2. Formulation
(Summarized from DDPG original paper)
Assumptions:
• An agent interacting with the environment in discrete timesteps;
• Actions are real-valued ![]() ;
;
• Environment is fully-observed ![]() .
.
Agent’s Goal: learn a policy which maximizes the expected return from the start distribution:
![]()
![]()
Ignore the inner expectation, we get:
![]()
There are two ways of learning off-policy: using a replay-buffer or by important sampling.
In the traditional commonly used Q-learning, as an off-policy algorithm, it just uses the greedy policy, regardless of
![]()
![]()
![]()
Conclusion: DQN solves the problem of learning large, no-linear function approximator problem by introducing the replay buffer and the target network, however, the problem of agent taking continuous actions will be solved idea from the DPG algorithm.
DPG algorithm recap:
The DPG algorithm maintains a parameterized actor function ![]() which specifies the current policy by deterministically mapping states to a specific action. The critic
which specifies the current policy by deterministically mapping states to a specific action. The critic ![]() is learned by using the Bellman equation as in Q-learning. The actor is updated by following the chain rule to the expected return from the start distribution
is learned by using the Bellman equation as in Q-learning. The actor is updated by following the chain rule to the expected return from the start distribution ![]() with respect to the policy parameters:
with respect to the policy parameters:
![]()
NFQCA uses the same update rules as DPG but with neural network function approximators, and uses batch learning for stability, which is intractable for large networks.
DDPG using ideas from DQN to solve this stability problem.
Other problems: Problems of using neural network in reinforcement learning, training supervised learning neural network, the training samples is assumed to be independently and identically distributed.
Replay Buffer solve two problems: learning neural networks from sequentially generated samples; feasibility of learning large no-linear problem.
Key Points:
Replay buffer for de-correlating samples:
As in DQN, the replay buffer is a finite size cache
Target network for learning stability:
Target network is a little different from that in DQN and is modified for actor-critic to use ‘soft’ target updates, rather than directly copying the weights. DDPG create a copy of the actor and critic networks, namely, the actor target network and the critic target network
Batch normalization to improve generalization:
Why batch normalization is proposed? (To solve the generation problem or physical units scaling) For different tasks, different components of the observation may have different physical units (for example, positions versus velocities) and the ranges may vary across environments. This can make it difficult for the network to learn effectively and may make it difficult to find hyper-parameters which generalize across environments with different scales of state values.
In the low-dimensional case, we used batch normalization on the state input and all layers of the
Exploration Exploitation:
Using the exploration policy:
![]()
3. Pseudocode and Code Implementation
OpenAI Spinning-up Modified version according to the corresponding documentation: (selected from OpenAI Spinning-up)
This section is drawn from OpenAI SpiningUp Documentation which provides a much clearer and excellent explanation of how DDPG worker.
3.1 The Q-Learning Side of DDPG:
According to the Bellman equation describing the optimal action-value function ![]() :
:
![]()
The Bellman equation is used to learn an approximator to
![]()
Replay Buffers: In order for the algorithm to have stable behavior, the replay buffer should be large enough to contain a wide range of experiences, but it may not always be good to keep everything. If you only use the very-most recent data, you will overfit to that and things will break; if you use too much experience, you may slow down your learning. This may take some tuning to get right. (Tips: We’ve mentioned that DDPG is an off-policy algorithm: this is as good a point as any to highlight why and how. Observe that the replay buffer should contain old experiences, even though they might have been obtained using an outdated policy. Why are we able to use these at all? The reason is that the Bellman equation doesn’t care which transition tuples are used, or how the actions were selected, or what happens after a given transition, because the optimal Q-function should satisfy the Bellman equation for all possible transitions. So any transitions that we’ve ever experienced are fair game when trying to fit a Q-function approximator via MSBE minimization.)
Target Networks: In the Q-learning algorithms, the target is defined as
![]()
In DQN-based algorithms, the target network is just copied over from the main network every some-fixed-number of steps. In DDPG-style algorithms, the target network is updated once per main network update by polyak averaging:
![]()
DDPG Detail: Calculating the Max Over Actions in the Target. As mentioned earlier: computing the maximum over actions in the target is a challenge in continuous action spaces. DDPG deals with this by using a target policy network to compute an action which approximately maximizes
Putting it all together, Q-learning in DDPG is performed by minimizing the following MSBE loss with stochastic gradient descent:
![]()
3.2 The Policy Learning Side of DDPG:
The policy learning in DDPG tends to learn a deterministic policy
Note that the Q-function parameters are treated as constants here.
3.3 Exploration & Exploitation:
DDPG trains a deterministic policy in an off-policy way. Because the policy is deterministic, if the agent were to explore on-policy, in the beginning it would probably not try a wide enough variety of actions to find useful learning signals. To make DDPG policies explore better, we add noise to their actions at training time. The authors of the original DDPG paper recommended time-correlated OU noise, but more recent results suggest that uncorrelated, mean-zero Gaussian noise works perfectly well. Since the latter is simpler, it is preferred.
Version 1
The OpenAI spinning up DDPG pseudocode is as follow:
 Corresponding Code is modified from original OpenAI Spinning Up Git, but encapsulate all modules into a single file to faicilitate implementation and understanding:
Corresponding Code is modified from original OpenAI Spinning Up Git, but encapsulate all modules into a single file to faicilitate implementation and understanding:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 |
import numpy as np import tensorflow as tf import gym import time def placeholder(dim=None): return tf.placeholder(dtype=tf.float32, shape=(None,dim) if dim else (None,)) def placeholders(*args): return [placeholder(dim) for dim in args] def mlp(x, hidden_sizes=(32,), activation=tf.tanh, output_activation=None): for h in hidden_sizes[:-1]: x = tf.layers.dense(x, units=h, activation=activation) return tf.layers.dense(x, units=hidden_sizes[-1], activation=output_activation) def get_vars(scope): return [x for x in tf.global_variables() if scope in x.name] def count_vars(scope): v = get_vars(scope) return sum([np.prod(var.shape.as_list()) for var in v]) """Actor-cirtics""" def mlp_actor_critic(x, a, hidden_sizes=(256, 256), activation=tf.nn.relu, output_activation=tf.tanh, action_space=None): act_dim = a.shape.as_list()[-1] act_limit = action_space.high[0] with tf.variable_scope('pi'): pi = act_limit * mlp(x, list(hidden_sizes)+[act_dim], activation, output_activation) with tf.variable_scope('q'): q = tf.squeeze(mlp(tf.concat([x,a], axis=-1), list(hidden_sizes)+[1], activation, None), axis=1) with tf.variable_scope('q', reuse=True): q_pi = tf.squeeze(mlp(tf.concat([x,pi], axis=-1), list(hidden_sizes)+[1], activation, None), axis=1) return pi, q, q_pi class ReplayBuffer(object): """A simple FIFO experience replay buffer for DDPG agents. """ def __init__(self, obs_dim, act_dim, size): self.obs1_buf = np.zeros([size, obs_dim], dtype=np.float32) self.obs2_buf = np.zeros([size, obs_dim], dtype=np.float32) self.acts_buf = np.zeros([size, act_dim], dtype=np.float32) self.rews_buf = np.zeros(size, dtype=np.float32) self.done_buf = np.zeros(size, dtype=np.float32) self.ptr, self.size, self.max_size = 0, 0, size def store(self, obs, act, rew, next_obs, done): self.obs1_buf[self.ptr] = obs self.obs2_buf[self.ptr] = next_obs self.acts_buf[self.ptr] = act self.rews_buf[self.ptr] = rew self.done_buf[self.ptr] = done self.ptr = (self.ptr+1) % self.max_size self.size = min(self.size+1, self.max_size) def sample_batch(self, batch_size=32): idxs = np.random.randint(0, self.size, size=batch_size) return dict(obs1=self.obs1_buf[idxs], obs2=self.obs2_buf[idxs], acts=self.acts_buf[idxs], rews=self.rews_buf[idxs], done=self.done_buf[idxs]) def ddpg(env_fn, actor_critic=mlp_actor_critic, ac_kwargs=dict(), seed=0, steps_per_epoch=4000, epochs=100, replay_size=int(1e6), gamma=0.99, polyak=0.995, pi_lr=1e-3, q_lr=1e-3, batch_size=100, start_steps=10000, update_after=1000, update_every=50, act_noise=0.1, num_test_episodes=10, max_ep_len=1000): """ Deep Deterministic Policy Gradient (DDPG) env_fn: A function which creates a copy of the environment. The environment must satisfy the OpenAI Gym API. actor_critic: A function which takes in placeholder symbols for state, ``x_ph``, and action, ``a_ph``, and returns the main outputs from the agent's Tensorflow computation graph: =========== ================ ====================================== Symbol Shape Description =========== ================ ====================================== ``pi`` (batch, act_dim) | Deterministically computes actions from policy given states. ``q`` (batch,) | Gives the current estimate of Q* for | states in ``x_ph`` and actions in ``a_ph``. ``q_pi`` (batch,) | Gives the composition of ``q`` and | ``pi`` for states in ``x_ph``: q(x, pi(x)). =========== ================ ====================================== ac_kwargs (dict): Any kwargs appropriate for the actor_critic function provided to DDPG. seed (int): Seed for random number generators. steps_per_epoch (int): Number of steps of interaction (state-action pairs) for the agent and the environment in each epoch. epochs (int): Number of epochs to run and train agent. replay_size (int): Maximum length of replay buffer. gamma (float): Discount factor. (Always between 0 and 1.) polyak (float): Interpolation factor in polyak averaging for target networks. Target networks are updated towards main networks according to: .. math:: \\theta_{\\text{targ}} \\leftarrow \\rho \\theta_{\\text{targ}} + (1-\\rho) \\theta where :math:`\\rho` is polyak. (Always between 0 and 1, usually close to 1.) pi_lr (float): Learning rate for policy. q_lr (float): Learning rate for Q-networks. batch_size (int): Minibatch size for SGD. start_steps (int):Number of steps for uniform-random action selection,before running real policy.Helps exploration. update_after (int): Number of env interactions to collect before starting to do gradient descent updates. Ensures replay buffer is full enough for useful updates. update_every (int): Number of env interactions that should elapse between gradient descent updates. Note: Regardless of how long you wait between updates, the ratio of env steps to gradient steps is locked to 1. act_noise (float): Stddev for Gaussian exploration noise added to policy at training time. (At test time, no noise is added.) num_test_episodes (int): Number of episodes to test the deterministic policy at the end of each epoch. max_ep_len (int): Maximum length of trajectory / episode / rollout. """ tf.set_random_seed(seed) np.random.seed(seed) env, test_env = env_fn(), env_fn() obs_dim = env.observation_space.shape[0] act_dim = env.action_space.shape[0] # Action limit for clamping: critically, assumes all dimensions share the same bound! act_limit = env.action_space.high[0] # Share information about action space with policy architecture ac_kwargs['action_space'] = env.action_space # Inputs to computation graph x_ph, a_ph, x2_ph, r_ph, d_ph = placeholders(obs_dim, act_dim, obs_dim, None, None) # Main outputs from computation graph with tf.variable_scope('main'): pi, q, q_pi = actor_critic(x_ph, a_ph, **ac_kwargs) # Target networks with tf.variable_scope('target'): # Note that the action placeholder going to actor_critic here is # irrelevant, because we only need q_targ(s, pi_targ(s)). pi_targ, _, q_pi_targ = actor_critic(x2_ph, a_ph, **ac_kwargs) # Experience buffer replay_buffer = ReplayBuffer(obs_dim=obs_dim, act_dim=act_dim, size=replay_size) # Count variables var_counts = tuple(count_vars(scope) for scope in ['main/pi', 'main/q', 'main']) print('\nNumber of parameters: \t pi: %d, \t q: %d, \t total: %d\n'%var_counts) # Bellman backup for Q function backup = tf.stop_gradient(r_ph + gamma*(1-d_ph) * q_pi_targ) # DDPG losses pi_loss = -tf.reduce_mean(q_pi) q_loss = tf.reduce_mean((q - backup)**2) # Separate train ops for pi, q pi_optimizer = tf.train.AdamOptimizer(learning_rate=pi_lr) q_optimizer = tf.train.AdamOptimizer(learning_rate=q_lr) train_pi_op = pi_optimizer.minimize(pi_loss, var_list=get_vars('main/pi')) train_q_op = q_optimizer.minimize(q_loss, var_list=get_vars('main/q')) # Polyak averaging for target variables target_update = tf.group([tf.assign(v_targ, polyak*v_targ + (1-polyak)*v_main) for v_main, v_targ in zip(get_vars('main'), get_vars('target'))]) # Initializing targets to match main variables target_init = tf.group([tf.assign(v_targ, v_main) for v_main, v_targ in zip(get_vars('main'), get_vars('target'))]) sess = tf.Session() sess.run(tf.global_variables_initializer()) sess.run(target_init) def get_action(o, noise_scale): a = sess.run(pi, feed_dict={x_ph: o.reshape(1,-1)})[0] a += noise_scale * np.random.randn(act_dim) return np.clip(a, -act_limit, act_limit) def test_agent(): for j in range(num_test_episodes): o, d, ep_ret, ep_len = test_env.reset(), False, 0, 0 while not(d or (ep_len==max_ep_len)): # Take deterministic actions at test time (noise_scale=0) o, r, d, _ = test_env.step(get_action(o, 0)) ep_ret += r ep_len += 1 print('#TestEpRet: {}, TestEpLen: {}'.format(ep_ret, ep_len)) # Prepare for interaction with environment total_steps = steps_per_epoch * epochs # start_time = time.time() o, ep_ret, ep_len = env.reset(), 0, 0 # Main loop: collect experience in env and update/log each epoch for t in range(total_steps): # Until start_steps have elapsed, randomly sample actions from a uniform distribution for # better exploration. Afterwards, use the learned policy (with some noise, via act_noise). if t > start_steps: a = get_action(o, act_noise) else: a = env.action_space.sample() # Step the env o2, r, d, _ = env.step(a) ep_ret += r ep_len += 1 # Ignore the "done" signal if it comes from hitting the time horizon (that is, when it's an # artificial terminal signal that isn't based on the agent's state) d = False if ep_len==max_ep_len else d # Store experience to replay buffer replay_buffer.store(o, a, r, o2, d) # Super critical, easy to overlook step: make sure to update most recent observation! o = o2 # End of trajectory handling if d or (ep_len == max_ep_len): print('#MainEpRet={}, MainEpLen={}'.format(ep_ret, ep_len)) o, ep_ret, ep_len = env.reset(), 0, 0 # Update handling if t >= update_after and t % update_every == 0: for _ in range(update_every): batch = replay_buffer.sample_batch(batch_size) feed_dict = {x_ph: batch['obs1'], x2_ph: batch['obs2'], a_ph: batch['acts'], r_ph: batch['rews'], d_ph: batch['done']} # Q-learning update outs = sess.run([q_loss, q, train_q_op], feed_dict) # print('LossQ={}, QVals={}'.format(outs[0], outs[1])) # Policy update outs = sess.run([pi_loss, train_pi_op, target_update], feed_dict) # print('LossPi={}'.format(outs[0])) # End of epoch wrap-up if (t + 1) % steps_per_epoch == 0: # epoch = (t + 1) // steps_per_epoch # Test the performance of the deterministic version of the agent. test_agent() if __name__ == '__main__': # env = 'HalfCheetah-v2' env = 'MountainCarContinuous-v0' hid = 256 l = 2 gamma = 0.99 seed = 0 epochs = 50 exp_name = 'ddpg' ddpg(lambda : gym.make(env), actor_critic=mlp_actor_critic, ac_kwargs=dict(hidden_sizes=[hid]*l), gamma=0.99, seed=seed, epochs=epochs) |
The result is as follow: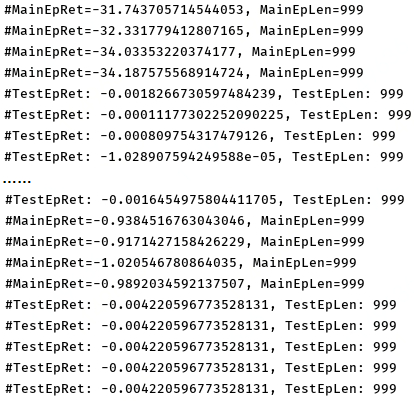
Version 2
I draw a diagram to illustarte the iteration process: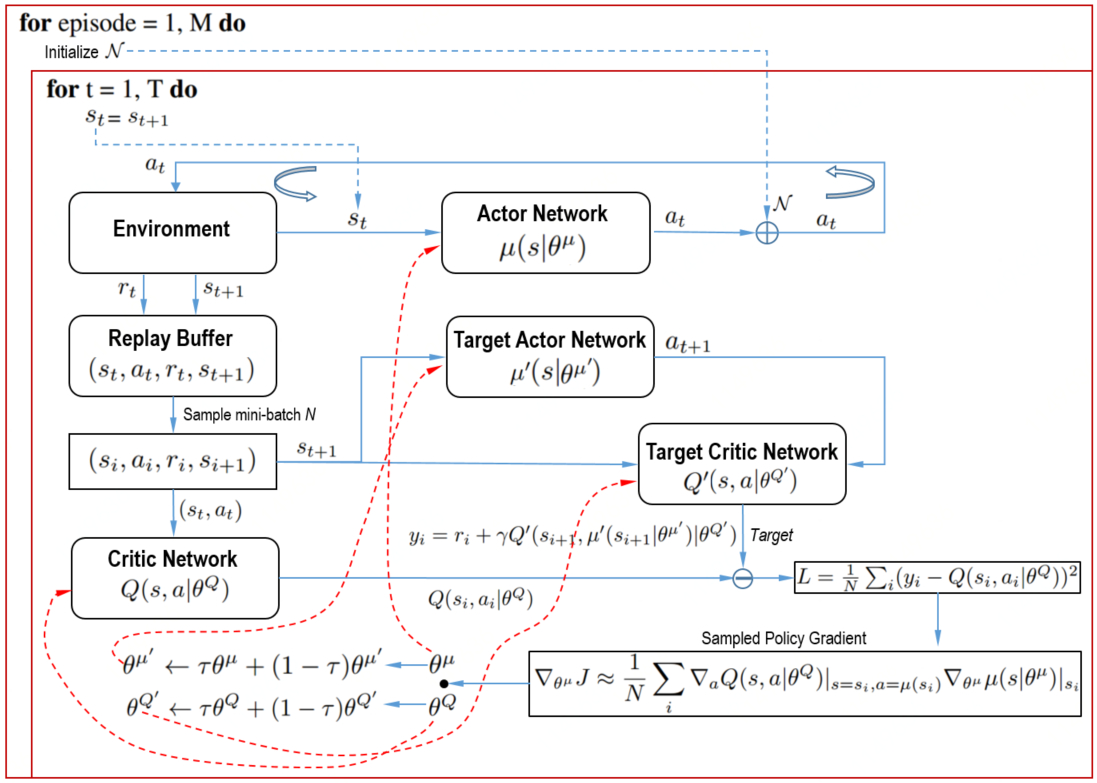 DDPG alogrithm pseudocode from original DDPG paper and correspondng a minimal implementation:
DDPG alogrithm pseudocode from original DDPG paper and correspondng a minimal implementation:
Code implementation
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 |
import gym import random import collections import torch import torch.nn as nn import torch.nn.functional as F import torch.optim as optim import numpy as np lr_mu = 0.0005 lr_q = 0.001 gamma = 0.99 batch_size = 32 buffer_limit = 50000 tau = 0.005 # for target network soft update class ReplayBuffer(object): def __init__(self): self.buffer = collections.deque(maxlen=buffer_limit) def put(self, transition): self.buffer.append(transition) def sample(self, n): mini_batch = random.sample(self.buffer, n) s_lst, a_lst, r_lst, s_prime_lst, done_mask_lst = [], [], [], [], [] for transition in mini_batch: s, a, r, s_prime, done_mask = transition s_lst.append(s) a_lst.append([a]) r_lst.append([r]) s_prime_lst.append(s_prime) done_mask_lst.append([done_mask]) return torch.tensor(s_lst, dtype=torch.float), torch.tensor(a_lst), torch.tensor(r_lst), \ torch.tensor(s_prime_lst, dtype=torch.float), torch.tensor(done_mask_lst) def size(self): return len(self.buffer) class MuNet(nn.Module): def __init__(self): super(MuNet, self).__init__() self.fc1 = nn.Linear(3, 128) self.fc2 = nn.Linear(128, 64) self.fc_mu = nn.Linear(64, 1) def forward(self, x): x = F.relu(self.fc1(x)) x = F.relu(self.fc2(x)) mu = torch.tanh(self.fc_mu(x))*2 # Multipled by 2 because the action space of the Pendulum-v0 is [-2,2] return mu class QNet(nn.Module): def __init__(self): super(QNet, self).__init__() self.fc_s = nn.Linear(3, 64) self.fc_a = nn.Linear(1, 64) self.fc_q = nn.Linear(128, 32) self.fc_3 = nn.Linear(32, 1) def forward(self, x, a): h1 = F.relu(self.fc_s(x)) h2 = F.relu(self.fc_a(a)) cat = torch.cat([h1, h2], dim=1) q = F.relu(self.fc_q(cat)) q = self.fc_3(q) return q class OrnsteinUhlenbeckNoise(object): def __init__(self, mu): self.theta, self.dt, self.sigma = 0.1, 0.01, 0.1 self.mu = mu self.x_prev = np.zeros_like(self.mu) def __call__(self): x = self.x_prev + self.theta * (self.mu - self.x_prev) * self.dt + \ self.sigma * np.sqrt(self.dt) * np.random.normal(size=self.mu.shape) self.x_prev = x return x def train(mu, mu_target, q, q_target, memory, q_optimizer, mu_optimizer): s, a, r, s_prime, done_mask = memory.sample(batch_size) target = r + gamma * q_target(s_prime, mu_target(s_prime)) q_loss = F.smooth_l1_loss(q(s,a), target.detach()) q_optimizer.zero_grad() q_loss.backward() q_optimizer.step() mu_loss = -q(s, mu(s)).mean() mu_optimizer.zero_grad() mu_loss.backward() mu_optimizer.step() def soft_update(net, net_target): for param_target, param in zip(net_target.parameters(), net.parameters()): param_target.data.copy_(param_target.data * (1.0 - tau) + param.data * tau) def main(): env = gym.make('Pendulum-v0') memory = ReplayBuffer() q, q_target = QNet(), QNet() q_target.load_state_dict(q.state_dict()) mu, mu_target = MuNet(), MuNet() mu_target.load_state_dict(mu.state_dict()) score = 0.0 print_interval = 20 mu_optimizer = optim.Adam(mu.parameters(), lr=lr_mu) q_optimizer = optim.Adam(q.parameters(), lr=lr_q) ou_noise = OrnsteinUhlenbeckNoise(mu=np.zeros(1)) for n_epi in range(10000): s = env.reset() for t in range(300): a = mu(torch.from_numpy(s).float()) a = a.item() + ou_noise()[0] s_prime, r, done, info = env.step([a]) memory.put((s, a, r/100.0, s_prime, done)) score += r s = s_prime if done: break if memory.size()>2000: for i in range(10): train(mu, mu_target, q, q_target, memory, q_optimizer, mu_optimizer) soft_update(mu, mu_target) soft_update(q, q_target) if n_epi%print_interval==0 and n_epi!=0: print('# of episode :{}, avg score: {:.1f}'.format(n_epi, score/print_interval)) score = 0.0 env.close() if __name__ == '__main__': main() |
The result is as follow: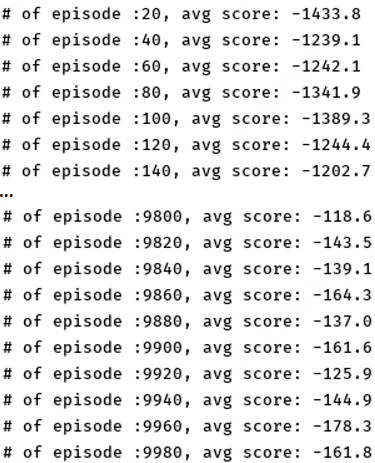
4. Reference
1. Continuous Control With Deep Reinforcement Learning, Lillicrap et al. 2016
2. OpenAI Spinning Up Documentation, DDPG